Introducción
El objetivo de la presente investigación es describir a grandes rasgos la teoría de las distribuciones estables multivariadas, con el objetivo de estimar un modelo GARCH multivariado estable sub-Gaussiano, que posteriormente se aplica en la estimación del VaR de un portafolio.
El creciente interés en el uso de las distribuciones α-estable o estables ha sido motivado por sus diversas aplicaciones a problemas prácticos, entre ellos, su aplicación en el modelo de portafolios financieros. A partir de los trabajos seminales de Mandelbrot (1963) y Fama (1965), los modelos estables que describen los rendimientos de activos financieros han ido ocupando un lugar prominente tanto en estadística como en la literatura financiera (por ejemplo: Rachev y Han, 2000; Mittnik y Rachev, 1989, Rachev y Mittnik, 2000; Panorska, Mittnik y Rachev, 1995; Mittnik, Rachev y Paolella, 1997).
Las distribuciones estables son de interés, debido a que el Teorema del Límite Central Generalizado afirma que el único límite no trivial de sumas de variables aleatorias normalizadas independientes e idénticamente distribuidas (i.i.d.), es estable. Es decir, los vectores aleatorios estables poseen la propiedad que cualquier combinación lineal de sus componentes es α-estable, lo cual es una característica muy útil en la teoría de portafolios, ya que bajo el supuesto de que los rendimientos de los activos siguen una distribución estable conjunta, entonces el rendimiento de cualquier portafolio de estos activos también sigue una distribución α-estable.
Por otro lado, en el manejo de riesgos, el principal interés es modelar el caso extremo de las posibles pérdidas. A partir de las investigaciones empíricas, sabemos que una pérdida extrema en un activo, muy a menudo conduce a altas pérdidas en muchos otros activos. Este comportamiento del mercado no puede ser modelado por la distribución normal, pero con ciertas distribuciones elípticas, como por ejemplo, la distribución α-estable sub-Gaussiana, podemos capturar este comportamiento.
Sin embargo, y aunque el problema de estimación de los parámetros en el caso univariado ha sido resuelto satisfactoriamente (ver McCulloch, 1986; Nolan, 2001), hasta ahora, la literatura sobre la distribución estable multivariada es escasa.
El principal obstáculo en la implementación de modelos estables es la ausencia de expresiones analíticas explícitas para la función de densidad de probabilidad (excepto las distribuciones de Gauss, Cauchy y Levy). En el caso univariado, es posible utilizar la fórmula de inversión para recuperar la función de densidad de probabilidad (pdf, por sus siglas en inglés). En este contexto, el método basado en la transformada rápida de Fourier (FFT, por sus siglas en inglés) ha demostrado tener un buen desempeño en el cálculo de la densidad para un gran número de datos (ver Nolan, 1997; Mittnik, Doganoglu y Chenyao, 1999; Khindanova, Rachev y Schwartz, 2001). Desafortunadamente, en el caso multivariado, el cálculo de la pdf es aún más complicado. La función característica conjunta general implica el cálculo de una integral con respecto a la llamada medida espectral, es decir, una medida de Borel finita sobre la esfera unitaria , donde d representa la dimensión del vector estable multivariado.
Hasta hoy, algunos casos específicos dentro del caso general han sido resueltos. Un método para estimar los parámetros de un portafolio estable se describe en Press (1972). Modarres y Nolan (1994) presentan un método para simular vectores aleatorios estables multivariados. Byczkowski, Nolan, y Rajput (1993) y Nolan y Rajput (1997) describen un método para aproximar medidas espectrales estables mediante una medida discreta, además del cálculo numérico de la densidad estable multivariada. Por otro lado, Nolan, Panorska y McCulloch (2001) presentan dos métodos de estimación de las medidas espectrales, uno basado en la función característica empírica y otro en las proyecciones unidimensionales de los datos.
Además, Mittnik y Rachev (1993) sugieren un método para estimar el exponente característico y la medida espectral de una distribución estable bivariada generalizada, empleando solo un pequeño subconjunto de datos extraídos de las colas extremas. McCulloch (2000) presenta un método para estimar la medida espectral de una distribución estable bivariada generalizada, basada en la serie de estimaciones de los parámetros estable de las proyecciones univariadas de todo el conjunto de datos, obtenidas por máxima verosimilitud. La correspondiente densidad espectral estable es obtenida mediante programación cuadrática.
El primer objetivo de esta investigación es proponer un modelo de volatilidad multivariable, el cual combina la propiedad de la distribución α-estable para modelar colas pesadas con el modelo GARCH para capturar clúster de volatilidad. El supuesto inicial es que condicionalmente los rendimientos siguen una distribución sub-Gaussiana, la cual es un caso particular de las distribuciones estables multivariadas.
Esta opción permite trabajar con una expresión de la función característica multivariada manejable. A diferencia de Bonato (2012), quien emplea un modelo GARCH multivariado bajo la hipótesis sub-Gaussiana restringido a dos dimensiones, en la presente investigación, el modelo propuesto se aplica a un portafolio compuesto por 5 activos pertenecientes a la Bolsa Mexicana de Valores (BMV).
El segundo objetivo es aplicar el modelo GARCH, propuesto en la estimación del VaR bajo la hipótesis α-estable sub-Gaussiana, a un portafolio compuesto por 5 activos que cotizan en la BMV.
Finalmente, dado que no hay evidencia empírica sobre el desempeño de los modelos VaR en la medición de riesgo durante períodos de alta volatilidad en los precios de los activos en el mercado financiero mexicano, se realiza una prueba de desempeño del VaR (backtesting), la cual permite analizar y comparar el desempeño del modelo propuesto con la estimación del VaR obtenida bajo la hipótesis multivariada Gaussiana, t-Student y Cauchy durante el período de la crisis financiera de 2008.
La principal contribución de este trabajo es que proporciona evidencia acerca de que las estimaciones del VaR mediante el modelo GARCH multivariado, bajo la hipótesis α-estable sub-Gaussiana, muestran un mejor desempeño durante períodos de turbulencias financieras.
El resto del documento se organiza de la siguiente forma: en la sección 2, se presenta una breve descripción teórica de las distribuciones estables multivariadas. La sección 3 proporciona una descripción de la distribución multivariada α-estable sub-Gaussiana y su respectiva estimación. El modelo GARCH multivariado sub-Gaussiano propuesto es descrito en la sección 4. En la sección 5, se presenta el análisis del comportamiento elíptico de los datos, la estimación de la matriz de dispersión, los resultados del modelo GARCH multivariado estable sub-Gaussiano y su respectiva aplicación, en el cálculo del VaR -por lo que se sabe, por primera vez- a un portafolio compuesto por acciones de la BMVM, y la valuación de su desempeño se describe en la sección 6. El documento finaliza con las conclusiones y sugerencias de posibles líneas de investigación.
1. Distribuciones estables multivariadas
Definición. Un vector aleatorio d-dimensional es estable si, para todo , existe una constante y un vector , tal que:
,
donde son copias i.i.d. de La constante debe ser de la forma , donde es el índice de estabilidad.
Algunas veces es utilizado el término conjuntamente estable para subrayar el hecho de que todas las componentes del vector estable deben ser α-estable univariadas1, bajo un mismo índice de estabilidad Esto se deduce del siguiente teorema, y justifica el uso del término vector aleatorio α-estable.
Teorema. i) Sea un vector aleatorio estable. Entonces toda proyección unidimensional es una variable aleatoria estable unidimensional, con el mismo índice para todo
ii) Inversamente, supongamos que es un vector aleatorio con la propiedad de que toda proyección unidimensional es estable, lo cual se denota como Entonces, existe un único , el cual es el índice de estabilidad de todas las proyecciones, es decir, es constante. Si entonces es estable. Si , y la función y el vector de parámetros de localización o posición de los componentes (todos en la 1-parametrización) están relacionados por:
entonces, es estable.
La demostración de la primera parte de este teorema es la demostración del Teorema 2.1.2 de Samorodnitsky y Taqqu (1994), la segunda es la demostración del Teorema 2.1.5 (c) de Samorodnitsky y Taqqu (1994) cuando la demostración del caso se encuentra en Nolan (1999).
Una ventaja del teorema anterior es que proporciona una forma de parametrizar las distribuciones estables multivariadas en términos de proyecciones unidimensionales. Es decir, conociendo la función característica de para todo , es posible conocer la función característica de Por lo cual, y las funciones caracterizan completamente la distribución conjunta. De hecho, conociendo estas funciones sobre la esfera unitaria , es posible caracterizar la distribución.
Otra ventaja del teorema, es que proporciona una forma de evaluar si un conjunto de datos multivariables es estable, examinando solo las proyecciones unidimensionales de los datos. Se realizan proyecciones en múltiples direcciones, y se observa si estas son bien descritas por distribuciones estables univariadas. Si es así, y el índice de estabilidad es el mismo para todas las direcciones (si el parámetro de posición, satisface (1)), entonces un modelo estable multivariado es apropiado.
1.1. Medida espectral
Una alternativa para describir vectores aleatorios α-estable es su medida espectral (una medida de Borel finita sobre la esfera unitaria en ) y un vector de localización
La demostración del siguiente resultado, el cual se le atribuye a Feldheim (1937), aparece en la sección 2.3 de Samorodnitsky y Taqqu (1994), en él se escriben las funciones y , en términos de la medida espectral.
Teorema. Sea un vector aleatorio conjuntamente estable, tal que:
para todo Entonces, existe una medida finita sobre y un vector de localización , en términos de los cuales es posible reescribir los parámetros de escala , de asimetría y de posición cuando
Para todo , la proyección es una variable aleatoria estable uno dimensional.
2. Distribuciones multivariadas α-estable Sub-Gaussianas o Elípticas
Desafortunadamente, ajustar distribuciones α-estable multivariadas a los datos en el caso de dimensiones mayores a 2 aún no es factible, dado que la medida espectral de la función característica es extremadamente difícil de estimar (ver Cheng y Rachev, 1995; Nolan, Panorska y McCulloch, 2001); pero algunos casos especiales son computacionalmente accesibles.
En esta investigación, son tomadas en cuenta las distribuciones multivariadas α-estable sub-Gaussianas o Elípticas, las cuales son una subclase del caso general, por lo cual satisfacen el Teorema del Límite Central generalizado, lo cual las hace atractivas en la teoría financiera.
2.1. Vectores aleatorios α-estable sub-Gaussianos
Si es un vector α-estable sub-Gaussiano o simplemente elíptico, entonces tiene la función característica
y parámetros de proyección:
,
donde es una matriz definida positiva y es el vector de localización. En este caso, la medida espectral es complicada (Proposición 2.5.8 de Samorodnitsky y Taqqu, 1994).
Sea un vector aleatorio multivariado normal dimensional con media nula y matriz de varianza-covarianza independiente de una variable aleatoria α/2-estable totalmente sesgada a la derecha con Entonces,
es un vector multivariado α-estable sub-Gaussiano con función característica conjunta
.
En particular, si y entonces
tiene función característica (2).
El vector multivariado α-estable sub-Gaussiano hereda su estructura de dependencia del vector subyacente aleatorio multivariado normal la cual es descrita por la matriz de varianza-covarianza , también llamada matriz de dispersión.
2.2. Estimación de la distribución α-estable sub-Gaussiana multivariada
Como se mencionó anteriormente, la estimación de los parámetros de la distribución α-estable sub-Gaussiana es posible. Sea un vector multivariado α-estable sub-Gaussiano, se propone el siguiente algoritmo para estimar los parámetros que lo describen:
1) Para cada una de las componentes del vector α-estable sub-Gaussiano , estimar el vector de parámetros
2) Estimar el índice de estabilidad de la distribución multivariada de la siguiente forma:
3) Centrar la distribución substrayéndole a el parámetro de posición estimado
4) Estimar la matriz de dispersión
2.2.1. Estimación de la matriz de dispersión
En el caso multivariado, es de suma importancia modelar la estructura de dependencia entre los activos que conforman el portafolio, desafortunadamente, la matriz de varianza-covarianza de los rendimientos no está definida en el caso de las distribuciones estables cuando . En cambio, bajo la hipótesis sub-gaussiana, el parámetro de escala del vector multivariado se puede escribir como una combinación lineal de la matriz de covarianza de los vectores gaussianos subyacentes, lo cual nos permite estimar la matriz de dispersión .
En esta investigación, se estima la matriz de dispersión siguiendo el método de la proyección propuesto por Nolan (2013), en el que los parámetros de la distribución estable multivariada son funciones explícitas de los parámetros de cada una de las series univariadas, los cuales son estimados vía máxima verosimilitud. A continuación, se hace una breve descripción de este método:
Dado , un vector aleatorio α-estable sub-Gaussiano dimensional, se tiene que para cualquier vector la proyección es α-estable univariada con parámetro de escala . Por lo cual,
En particular, los elementos de la diagonal de la matriz de dispersión son el cuadrado del parámetro de escala del i-ésimo componente de ; es decir, , donde representa la base canónica; y , donde es el parámetro de escala de la proyección Esto implica estimar parámetros de escala unidimensionales.
Dado que el vector multivariado α-estable sub-Gaussiano hereda su estructura de dependencia del vector subyacente aleatorio multivariado normal Kring, Rachev, Markus y Fabozzi (2009) señalan que es posible interpretar como la cuasi-varianza del componente , y como la cuasi-varianza entre los componentes y
3. Modelo GARCH multivariado elíptico o sub-Gaussiano estable
La extensión del caso multivariado de los modelos Autorregresivo con Heterocedasticidad Condicional (ARCH), introducido por Engle (1982), y el modelo ARCH generalizado o GARCH, propuesto por Bollerslev (1986) para describir la heteroscedasticidad de las variables financieras, ha sido prolífico. Sin embargo, la mayoría de estos modelos descansan en el supuesto de que los datos siguen una distribución normal multivariada o t-student, por lo cual es posible describir la estructura de dependencia de los activos mediante la matriz de varianza-covarianza.
La aplicación de las distribuciones estables en los modelos GARCH es relativamente nueva. Panorska, Mittnik y Rachev (1995); Mittnik, Paolella y Rachev (2002); Curto, Pinto y Tavares (2009); Bonato (2012), Naka y Oral (2013); y Mohammadi (2017) emplean modelos GARCH con distribuciones estables para examinar la volatilidad de los rendimientos financieros. En esta investigación, se propone un modelo GARCH multivariado elíptico o sub-Gaussiano, donde la estructura de dependencia de los activos es descrita mediante la matriz de dispersión, lo cual nos permite reducir los cálculos numéricos. El modelo se describe a continuación.
Definamos como el vector de las innovaciones de los rendimientos. Supongamos que es un vector α-estable sub-Gaussiano, es decir , donde es una variable aleatoria α/2-estable, totalmente sesgada a la derecha con y , un vector aleatorio multivariado normal dimensional con media nula y matriz de varianza-covarianza independiente de
Por lo cual, el vector de rendimientos del portafolio , donde representa los pesos del portafolio, es un vector α-estable sub-Gaussiano con parámetros de proyección Lo cual, es consecuencia directa del Teorema del Límite Central Generalizado.
El índice de estabilidad del portafolio no se estimará directamente de la distribución de los rendimientos del mismo, pues hacerlo de esta forma no sería adecuado, dado que no se consideraría la estructura de dependencia y la heterocedasticidad condicional de los rendimientos. Por lo tanto, para considerar estas dos características previamente mencionadas, se propone introducir un modelo GARCH multivariante y estimar de la distribución de los rendimientos condicionales.
Siguiendo a Bonato (2012), optamos por el modelo GARCH multivariante con correlaciones condicionales dinámicas (DCC), propuesto por Engle (2002), debido a que su estimación es computacionalmente accesible y además es un modelo flexible que permite especificaciones distintas en los GARCH univariados, utilizados para calcular la matriz diagonal En esta investigación, la estimación de los GARCH univariados se realiza según el método descrito en Serrano y Mata (2018).
Engle (2002) define el modelo de la siguiente forma:
donde es el vector de medias condicionales, es la matriz de correlaciones condicionales, es la desviación estándar condicional de los GARCH univariados y es una matriz definida positiva , donde son los residuos estandarizados obtenidos de los GARCH univariados, es la matriz de covarianzas no condicionales de los residuos , y y son constantes positivas; el proceso presenta reversión a la media, siempre y cuando
En el modelo propuesto por Engle (2002), la hipótesis es que sigue una distribución gaussiana con matriz de covarianza , sin embargo, nuestra hipótesis es que los rendimientos siguen una distribución sub-Gaussiana estable, por lo cual en nuestro modelo propuesto, es reemplazada por la matriz de dispersión.
Como se mencionó previamente, la estimación de la matriz diagonal D t se efectúa empleando los modelos GARCH estable univariados, es decir es el parámetro de escala condicional del i-ésimo componente de y los elementos de la matriz R se estiman usando el método de la proyección propuesto por Nolan (2013).
De acuerdo con los trabajos de Mittnik, Paolella y Rachev (2002), y más recientemente Mohammadi (2017), lo anterior nos permite asegurar que nuestro modelo GARCH multivariado satisface las condiciones de estacionariedad.
Además, para estimar la matriz de dispersión empleamos el modelo propuesto por Nolan (2013), que se describe en la sección anterior, lo cual nos permite reducir los cálculos numéricos y por ende aumentar la rapidez de ejecución del algoritmo computacional. Esto nos da una ventaja sobre el modelo GARCH estable, propuesto por Bonato (2012), donde los cálculos numéricos son intensos, por lo cual su modelo solo se aplica a un portafolio bivariado; a diferencia de este, nuestro modelo es aplicado a un portafolio compuesto por 5 activos financieros.
4. Aplicación a la estimación del VaR de un portafolio compuesto por activos financieros que cotizan en la BMV
4.1. Descripción de los datos
Un portafolio es una combinación lineal de activos financieros (acciones, commodities, etc.). Considere un inversor que tiene una cantidad fija de dinero para invertir en activos: en el activo 1, en el activo 2,…, en el activo d. Las tasas de rendimiento, son aleatorias. Al concluir el período de inversión, el portafolio compuesto por estos activos tiene un rendimiento
La distribución de depende de la distribución del vector de rendimientos
Este trabajo propone el uso de distribuciones estables multivariadas, en particular el caso sub-Gaussiano, para estimar el VaR de un portafolio equiponderado; es decir, se asume que los componentes del portafolio siguen una distribución α-estable sub-Gaussiana. Algunos trabajos pioneros en esta área son Press (1972) y Cheng y Rachev (1995).
Para el análisis empírico, se han elegido 5 cinco activos con diferente volumen de operación que cotizan en la Bolsa Mexicana de Valores (BMV), pertenecientes a 5 diferentes industrias. Estos activos corresponden a las siguientes empresas: Consorcio ARA, S.A. de C.V. (ARA), líder en venta y construcción de inmuebles residenciales y que también opera como contratista para clientes no afiliados en la construcción, promoción y comercialización de proyectos comerciales e industriales; Controladora Comercial Mexicana (COMER), compañía controladora que opera en el sector detallista en México y cuenta con 199 tiendas y también con una cadena de 74 restaurantes familiares; Fomento Económico Mexicano, S.A.B. de C.V. (FEMSA), empresa que participa en la industria de refrescos, a través de Coca-Cola FEMSA, el embotellador independiente más grande de productos Coca-Cola en el mundo y también dispone de otras operaciones, como logística y equipo de refrigeración; Grupo Carso (GCARSO), uno de los conglomerados más importantes de América Latina que controla y opera empresas del sector industrial, comercial e infraestructura y construcción y Grupo Televisa, S.A.B. (TELEVISA), líder en la producción y transmisión de contenido de entretenimiento televisivo en México, involucrada en la producción de señales de televisión restringida, en servicios de televisión directa al hogar vía satélite, y en servicios de televisión por cable y telecomunicaciones. Se encarga también de la publicación y distribución de revistas, producción y transmisión de programas de radio, operación de un portal de Internet y en la industria de juegos y sorteos.
La moneda de referencia a utilizar en nuestro modelo es el peso mexicano, ya que es la moneda de cotización de las empresas. Las cinco series que conforman el portafolio de la aplicación, contienen información de los precios diarios de cierre de cada activo, excluyendo fines de semana y festivos.
La muestra total inicia el 2 de enero de 2003 y finaliza el 31 de diciembre de 2009, por lo cual se tienen 1767 observaciones, para cada uno de los activos. Esto con la finalidad de evaluar el desempeño de la estimación del modelo VaR α-estable durante períodos de alta volatilidad, como la crisis financiera de 2008. Además, para cada serie, se consideran los rendimientos logarítmicos diarios.
4.2. Análisis del comportamiento elíptico de los datos y estimación del índice de estabilidad
Primero determinemos si el portafolio puede ser descrito por una distribución α-estable sub-Gaussiana. Esto es de fundamental importancia, dado que cualquier portafolio bajo la hipótesis sub-Gaussiana es descrito por una distribución estable cuyo parámetro de escala es una combinación lineal de los elementos de la matriz de dispersión .
Lo anterior será analizado empleando el método propuesto por Nolan (2013), el cual se describe a continuación:
Estimar el vector de parámetros , para cada acción
Verificar que los índices de estabilidad estimados univariados no sean significativamente diferentes, dado que si esto ocurre, entonces los datos no son α-estable, conjuntamente, por lo cual no pueden ser modelados por una distribución sub-Gaussiana.
Verificar que los parámetros de asimetría estimados sean cercanos a cero, de lo contrario la distribución es no simétrica, por lo cual no podría ser sub-Gaussiana.
Utilizar gráficas de dispersión a pares para visualizar el comportamiento elíptico de los datos.
Si los datos cumplen los criterios 2-4, entonces el uso de un modelo sub-Gaussiano está justificado. En caso contrario, la hipótesis sub-Gaussiana se rechaza.
En este estudio, primero se filtraron los rendimientos logarítmicos empleando el modelo GARCH(1,1) multivariado sub-Gaussiano descrito anteriormente. Con lo cual se introdujo la heterocedasticidad de los rendimientos en el modelo multivariado. Posteriormente, se ajustaron los residuos condicionales al modelo sub-Gaussiano.
El modelo se describe a continuación:
En la tabla 1, se presentan la estimaciones del modelo GARCH(1,1) obtenidas por máxima verosimilitud.
Tabla 1.
Parámetros GARCH(1,1)
Fuente: Elaboración propia con datos de Bloomberg.
En la tabla 2, se presentan los parámetros estimados de la distribución α-estable para cada uno de los componentes del portafolio, los cuales son estimados por máxima verosimilitud mediante el programa STABLE, descrito en Nolan (1997).
Tabla 2.
Parámetros de la distribución α-estable sub-Gaussiana.
Nota. Entre paréntesis se tiene el error estándar y entre corchetes el estadístico t. Fuente: Elaboración propia.
En la tabla 2, se observa que los índices de estabilidad , son significativamente inferiores a 2, lo cual indica que los datos son leptocúrticos. Además, los índices de asimetría son cercanos a cero, excepto para la serie COMER y FEMSA, que resultan estadísticamente diferentes de cero según la metodología de Barndorff-Nielsen, Mikosch y Resnick (2012), ver apéndice A. Sin embargo, siguiendo la justificación presentada en Nolan (2013), página 2078, se justifica el uso de la distribución α-estable sub-Gaussiana.
Adicionalmente, se estiman los parámetros para las distribuciones multivariadas t-Student y Cauchy, con fines de comparación. Los resultados se encuentran en el apéndice B, donde cada estimador se acompaña de su error estándar y su estadístico de prueba t.
En las figuras 1 a 5, se muestran las gráficas de dispersión a pares de las acciones que componen el portafolio y se visualiza el comportamiento elíptico de los datos.
Dado que los datos cumplen los criterios 2-4, se concluye que estos siguen una distribución sub-Gaussiano multivariada. Por lo tanto, se procede a estimar el índice de estabilidad de la distribución multivariada usando (3) .
4.3. Estimación de matriz de dispersión
En esta sección, se muestra la matriz de dispersión estimada de la distribución α-estable sub-Gaussiana. Para estimarla se empleó el modelo descrito en la sección 2.2.1.
Antes de aplicar este modelo, se centra cada serie , substrayéndole el parámetro de posición estimado La matriz de dispersión estimada se muestra a continuación:
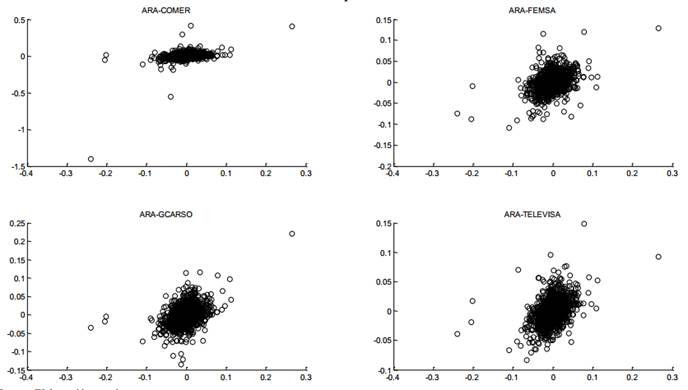
Fuente: Elaboración propia
Figura 1.
Gráfica de dispersión ARA
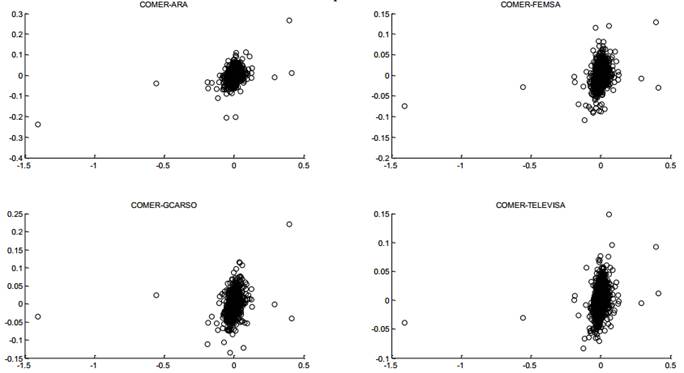
Fuente: Elaboración Propia
Figura 2.
Gráfica de dispersión COMMER
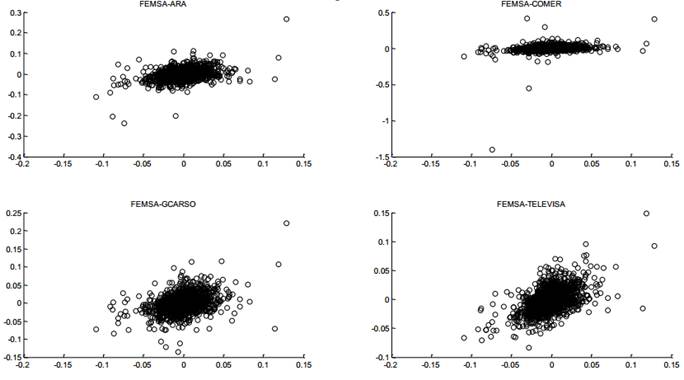
Fuente: Elaboración Propia
Figura 3.
Gráfica de dispersión FEMSA
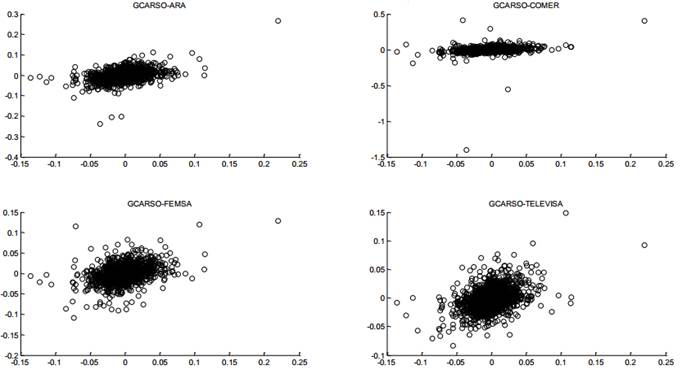
Fuente: Elaboración Propia
Figura 4.
Gráfica de dispersión GCARSO
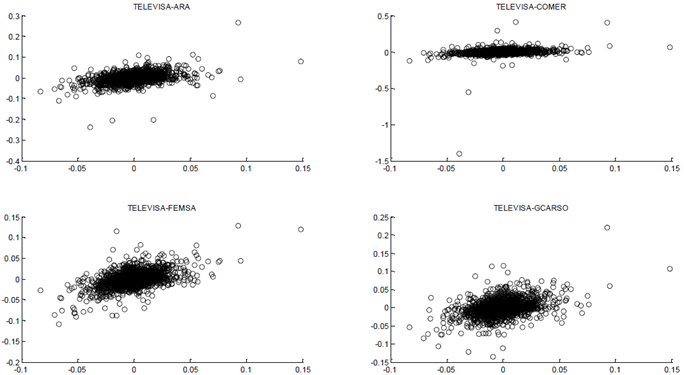
Fuente: Elaboración propia.
Figura.
Gráfica de dispersión TELEVISA
4.4. Estimaciones del VaR
En esta sección, se estima el VaR del portafolio mediante simulación Montecarlo, empleando el modelo GARCH multivariado sub-Gaussiano propuesto bajo la hipótesis de que: condicionalmente, los rendimientos siguen una distribución α-estable sub-Gaussiana.
El VaR se calcula considerando el horizonte de tiempo de un día y un nivel de confianza para lo cual se sigue el siguiente algoritmo:
Estimar los parámetros del modelo GARCH multivariado sub-Gaussiano, empleando el método de máxima verosimilitud y obtener los residuos condicionales.
Dados los residuos condicionales obtenidos en el paso anterior, estimar el índice de estabilidad de la distribución α-estable sub-Gaussiana.
Estimar la matriz de dispersión
Realizar simulaciones de vectores aleatorios α-estable sub-Gaussianos
Aplicar descomposición de Cholesky a
Generar los posibles escenarios .
Estimar los posibles rendimientos ,
Estimar el VaR como el negativo del q-esimo cuartil de la distribución de probabilidad simulada.
En la presente investigación, el VaR se estima a un nivel de confianza de 95%, 99% y 99.5%. En la tabla 3, se muestran los VaR estimados.
En las estimaciones del VaR, se observa que el modelo α-estable sub-Gaussiano proporciona valores mayores a las estimaciones basadas en la distribución normal, t-Student y Cauchy, es decir, el modelo del VaR α-estable sub-Gaussiano proporciona estimaciones de las pérdidas potenciales más conservadoras, lo cual es preferido por las instituciones financieras. Es importante señalar que este resultado corresponde al periodo 2008-2009.
Tabla 3.
Estimaciones del VaR
Fuente: Elaboración propia.
5. Evaluación del desempeño del VaR
5.1. Backtesting
En esta sección, se emplea la prueba llamada backtesting, para evaluar el desempeño del modelo VaR bajo el supuesto de que condicionalmente los rendimientos siguen una distribución α-estable sub-Gaussiana, t-Student, Cauchy y normal, respectivamente.
Sea el nivel de confianza para el cálculo del VaR y , el número de observaciones históricas más recientes empleadas para pronosticar el VaR actual. En este trabajo, k=502, es decir, utilizamos los datos históricos de los últimos dos años de la respectiva muestra para predecir el VaR.
El rango para el cual el número de veces que se ha excedido el VaR es aceptable y sus respectivas frecuencias a un nivel significativo del 1%, se muestran en la tabla 4.
Tabla 4.
Rango y frecuencia de violaciones del VaR aceptables.
| VaR | Rango de violaciones del VaR aceptable | Frecuencia de violaciones del VaR aceptable |
|---|---|---|
| 99.5% | [0,7] | [0.00%,1.31%] |
| 99.0% | [0,11] | [0.00%,2.14%] |
| 95.0% | [13,38] | [2.49%,7.51%] |
Fuente: Elaboración propia.
Los resultados del backtesting se muestran en la tabla 5. En esta tabla, se puede observar que durante el período de la crisis financiera de 2008, el número de violaciones del VaR bajo el supuesto de normalidad2 se encuentra muy por encima del intervalo admisible, lo que implica que el VaR, bajo este supuesto, subestima significativamente las pérdidas potenciales durante períodos de crisis.
Además, se observa que el número de violaciones del VaR, obtenida bajo la hipótesis multivariada t-Student y Cauchy, también exceden el rango aceptable, excepto la distribución multivariada t-Student para un nivel de confianza del 95%. En contraste, el número de violaciones del modelo VaR α-estable sub-Gaussiano se encuentra dentro del rango admisible de excepciones, durante el período de crisis; lo cual sugiere que este modelo tiene un mejor desempeño durante períodos de turbulencias financieras que el modelo VaR bajo la hipótesis multivariada Gaussiana, t-Student y Cauchy.
Tabla 5.
Backtesting del VaR.
5.2. Estadístico de Kupiec
Además, la evaluación del desempeño del VaR se realiza en términos de su probabilidad de cobertura empírica. Con este objetivo, se aplica la prueba de la razón de verosimilitud de Kupiec dada en Kupiec (1995), la cual estima si la proporción esperada de violaciones es igual al nivel de significancia α.
El estadístico de Kupiec es una prueba incondicional porque cuenta el número de violaciones durante todo el período. Además, como indica Kupiec (1995), las pruebas de cobertura incondicional tienen bajo poder con respecto a la hipótesis alternativa, si el tamaño de la muestra es pequeño; sin embargo, este problema no existe aquí, ya que en la presente investigación, la muestra seleccionada cubre un largo período de tiempo.
El estadístico de prueba de Kupiec para muestras grandes se distribuye como una Ji-cuadrada con un grado de libertad, y está dado por:
donde T representa el tamaño de la muestra, n el número de violaciones y p=n/T es el porcentaje de violaciones. La hipótesis nula se rechaza con un nivel de significancia del 1% si , es decir, si el valor del estadístico de Kupiec excede o es igual al valor crítico de una distribución Ji-cuadrada, con un grado de libertad y un nivel de significancia del 1%.
En la tabla 6, se presenta un resumen de los resultados de la prueba de la razón de verosimilitud de Kupiec (1995). El símbolo (X) se utiliza para indicar que el modelo VaR analizado cumple con la hipótesis de una cobertura incondicional correcta, es decir, el modelo se acepta como un modelo VaR bien especificado. Los modelos rechazados, debido a la sobreestimación o subestimación del VaR, se indican con asterisco (*) y signo menos (-), respectivamente.
Tabla 6.
Estadístico de Kupiec
Fuente: Elaboración propia.
En la tabla 6, se observa que el modelo VaR α-estable proporciona una cobertura incondicional correcta durante el período de crisis señalado. En contraste, el modelo VaR bajo las distribuciones normal y t-Student presentan un desempeño inferior durante el período de crisis, donde se sobrestima o subestima el VaR; salvo para el caso de la distribución de Cauchy al nivel de 95% de confianza.
Conclusiones
En esta investigación, se propuso un modelo GARCH α-estable sub-Gaussiano multivariado, el cual combina la propiedad de la distribución α-estable para modelar colas pesadas con el modelo GARCH, para capturar clúster de volatilidad. La finalidad fue comparar el desempeño de esta especificación, en relación con los casos de la distribución normal, Cauchy y t-Student.
En particular, se realizó la estimación del VaR bajo la hipótesis α-estable sub-Gaussiana durante el período de la crisis financiera de 2008, a partir de un portafolio compuesto por 5 activos financieros que cotizan en la BMV.
Los resultados estadísticos sugieren que el modelo VaR α-estable sub-Gaussiano proporciona estimaciones del VaR cuyas pruebas de backtesting tienen un mejor desempeño, en períodos de alta volatilidad; es decir, las estimaciones del VaR son más eficientes bajo el supuesto de que los rendimientos siguen una distribución α-estable sub-Gaussiana durante períodos de turbulencias financieras.
Sin embargo, es necesaria investigación adicional. Por ejemplo, sería conveniente considerar un conjunto mayor de distribuciones de probabilidad que también capturen las características empíricas de las series de datos financieros y comparar su desempeño con el modelo α-estable sub-Gaussiano aquí propuesto. Además, se podrían emplear funciones cópula para describir las correlaciones entre los rendimientos de las acciones, empleando tanto la distribución estable como la distribución marginal de los activos que conforman el portafolio.